Losing the World Record in HATETRIS
Tetris That Still Hates You
This is Part 2 of a series - it will make much more sense after reading Part 1. If you aren’t interested in reading Part 1, but still want this to make some semblance of sense, here’s what you need to know: HATETRIS is Tetris that hates you (and if you don’t know what Tetris is, this will make no sense), and we have been carefully exploring the deterministic space in which it lives, in pursuit of the world record. We achieved that in the last post with 86 points, a score we thought was a dozen points shy of the maximum possible score.
A quick recap of why HATETRIS is hateful: it will always pick the worst possible piece for you. When you play any version of Tetris, you want your well to be short, with as much empty space as possible. That’s why clearing lines is so helpful. HATETRIS wants your well to be tall, preferably so tall that your well goes over the ceiling, causing you to lose. It will always pick the piece which causes your well to be as tall as possible, even if you place that piece in the best available spot.
This is good, but it’s not perfect. In fact, Dr. Antoine Amarilli proved last year that there is NO perfectly hateful Tetris algorithm - it is always possible to get at least one point. So, as an additional safeguard, there is a final check. If giving you a certain piece would let you get back to a well you’ve already seen, HATETRIS will not give you that piece, to make sure you can’t create an infinite loop and play forever. Fortunately, the algorithm is so hateful anyway that this never comes up, and so programs like ours don’t have to waste time checking.
In the time between getting the 86 points and the next breakthrough in HATETRIS, we gave a talk about the specific Rust implementation details of our approach. If you want to hear us enthusiastically talk our way through things like mutexes, you can find it here.
And if you’d like to play around with the code we eventually made public, you can download it from GitHub here.
The Calm Before The Storm
There’s a point in any project, where you have reached the natural termination. Maybe you defended your thesis, maybe you got the world record, or maybe you discovered that barring breakthroughs in quantum computing, the whole idea is impractical. Regardless, it is the end. The point where you sit back, and calmly reflect, stripped of the blinding urgency that made putting all your code in a single function seem reasonable, and that let you hurtle down potential blind alleys with reckless abandon. It is “the calm”. For us, publishing part 1 of this blog post was that. We were done. Short of an offer from Google to work on UNDISCLOSED MACHINE LEARNING PROJECT we had done what we had set out to do.
The calm is the opportunity for reflection. To sit back and consider what approaches you took, why you took them, and to consider which directions you left unexplored. With the blog post and the talk behind us, we were able to do exactly that, to consider what we wish we had explored or done in our time. This is a moment of shining opportunity, because it’s a great chance to rekindle your interest and go explore those paths you left behind. For us, some of it was evaluating smaller wells again, and hypothesizing about machine learning approaches, as well as optimizations we might have missed. We discussed doing things on the GPU again, which we still thought would be way too hard. There was no real urgency, other than knewjade’s somewhat ominous tweets about HATETRIS.
From this period of reflection came some improvements to the emulator and a key idea that we called the “Bird in Hand” heuristic…
Non-Technical TL;DR
For the previous year and a half, throughout the whole project, we’d made the emulator faster by stripping away things that weren’t necessary. This new emulator, our final version, was the logical endpoint of that progression. We’d started off by storing HATETRIS moves and positions individually - by the time we were done with this section, we stored each position with just one single bit of information, the absolute minimum possible. The new emulator ran ten times faster than our old one, at a mere 5 μs per move, and ran almost a hundred thousand times faster per core than our very first Mathematica emulator, made in 2021.
The gist of how it works: rather than dealing with positions individually, we deal with groups of positions all at once; we call those groups of positions ‘waveforms’, and store them as 64-bit binary integers. Since CPUs can do operations on 64-bit binary integers in a single cycle, we can use each CPU cycle and each CPU operation to work on all of the positions, not just one at a time. This is efficient. It is also really cool.
When working with higher-level languages, one gets used to the idea that there’s a lot of CPU time going to waste. That this doesn’t matter. After all, you’re still going to get your answer in a few seconds. In a corporate environment, it’s going to the cloud anyway, you can just add more boxes. But for this project, we had just one computer to work with - we didn’t want to buy cloud computing time on Amazon again, like we did for the 86-point run. And the problem space is so large that it is not possible to buy enough computer power, for less than the GDP of a small country, to just brute-force away the inefficiencies. If we could calculate a billion moves per second, it would still take around 30 million years to explore every possible game.
The consequence? Every nanosecond of our one precious CPU became valuable, and we needed to make sure that it wasn’t spending any more of those nanoseconds than it had to. That’s why it was worth going this far down, stripping away this much excess and fat from our emulator, to make it as fast as it could possibly get. The technical details, for those interested, can be found in the appendix, but the important non-technical details can be summed up in a single graph:

This new emulator was fast.
A Bird in the Hand
Every order of magnitude brings qualitatively new effects. – Richard Hamming
In addition to the speed improvements, the new emulator gave us the ability to explore well sizes smaller or larger than the standard 20x10. This led to lots of faffing about with different well dimensions, seeing what kind of performance and what kind of scores we could get. The faffing in question was viable because, if it was a complete waste of time, it at least wasn’t a complete waste of very much time.
One of these tests was a narrow beam search for a 100x10 well with the heuristic we’d used for the previous world record. And that led to a very interesting result: the best strategy found was a setup that stacked pieces just about all the way to the ceiling, and then spent twenty-five moves clearing twenty-five consecutive lines. And that got us to thinking: what if we could encourage long setups for big payoffs in our actual heuristic, instead of long setups for big payoffs sometimes happening by accident?
A quick reminder, the current dominant search strategy while we were working on this was a heuristic driven beam search, in our own earlier words:
A ‘beam search’ means that you take some number of positions, get all of their children, keep the best ones, and then repeat the process until you run out of positions. For instance, if you had a beam search with a width of twenty-five million, then at every step, you take the best twenty-five million children from all of your existing wells, and use them as your wells for the next step. The ‘heuristic’ part is how you sort the children from best to worst in order to keep the best twenty-five million of them. link
Suppose you have a well labeled W_0. In Knewjade’s heuristic, if an S or a Z piece can be used to clear a line and create a new well W_1, then calculate the heuristics of both wells, H(W_0) and H(W_1), and take whichever value is better. Knewjade had noticed that the surface height could sometimes be moved down by an S or Z piece clearing a line, and wanted to encourage those line clears, even if the well looked bad at first glance.
So, following that logic, why stop at just one S or Z line clear? If you could clear a line with S, and then that new well could also clear a line with S (creating W_2), why not evaluate that second-generation well too? If that one too could clear a line with S, creating W_3), why not evaluate that third-generation well? It’s impossible to clear lines continuously forever, so why not keep going and going until there are no more line clears possible, and take the best out of all the children? The main argument against it is that “it would take a long time”, but as the emulator got faster, that was less and less of an issue.
The other obvious problem was that, looking so far ahead in the future, the heuristic might put off scoring indefinitely in favor of potentially scoring moves with S-pieces, and never get around to actually scoring. To answer this, we looked at the old proverbs, and heard that a bird in the hand is worth two in the bush. So, the potential scores were weighted at one-half of the actual scores (one bird in the bush would logically be worth one-half of a bird in the hand), and the heuristic would take whichever heuristic all of the S-cleared descendants was best. In essence, the heuristic now allowed for very long setups in exchange for very good payoffs.
There were minor tweaks to this basic idea that we made as we went; for instance, if an S piece could clear two lines, the HATETRIS emulator would never actually give that S piece, and so in that situation we’d check for wells cleared by Z pieces instead. David’s dad also took the wind out of our sails by telling us that we’d rediscovered what in chess programming was called the quiescent lookahead, and that this wasn’t a new technique we’d get to name after ourselves. But these were minor details; the core idea was what made all the difference.
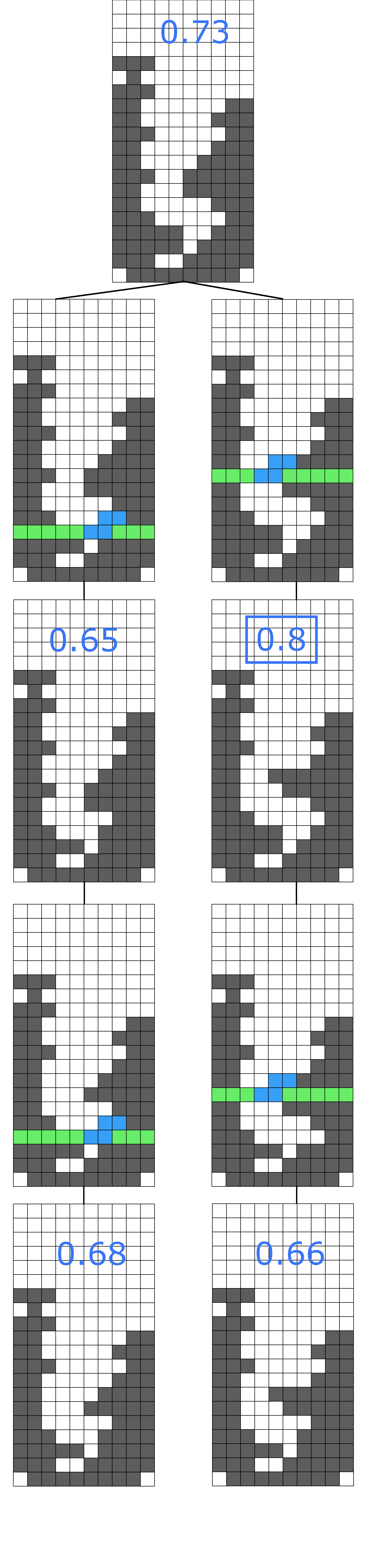
And this is where having a faster emulator made such a difference. For a beam width of 1 and 10 there was no improvement. For a beam width of 100, the score was 3 points higher. For a beam width of 1000, the score was 4 points higher, and for a beam width of 10,000, the score was just 3 points higher again…and at the cost of taking sixteen times longer to run. Sure, it was a slight improvement, but it was not nearly enough of an improvement to justify the extra runtime, since we could get a much bigger improvement by running a beam search multiple times wider. If 10,000 had taken an hour, we could have gone bigger, but we probably wouldn’t have bothered without some foreknowledge that it’d be worthwhile. But, 10,000 only took ten minutes, and so, why not? We ran it for 100,000.
And that’s where things took off. The best parameters we’d ever had, the parameters that got us the world record, got a score of 24 points with a width of 100,000. This new bird-in-the-hand lookahead got 62 points. That is not a typo. We got a score twice that of the 2017 world record, with a beam search less than half a percent as wide as the one we ran for 86 points.
So, obviously, we ran it for a million. And we got 148 points. Going all the way back to Atypical’s first 11-point game to start off the leaderboard, this was the largest ratio between a record and the previous record in HATETRIS history. The improvement over our previous record was 62 points, which would have been a very strong game in and of itself. As it was running, we speculated “maybe this will break the hundred point wall.” Even 110 points weren’t out of the question! But it wasn’t until we actually got 148 points that we believed that 148 points was even possible…and actually, not until well afterwards, since we at first feared that it was the result of an emulator bug. Only after we spent a full hour and a half entering in the game by hand (and vowing to automate replay writing, which we later did) did we genuinely believe that this score was real.

Even our most optimistic predictions didn’t see this coming. Of course, there were a lot of things we didn’t see coming…

Lookaheads
This is a good place to reflect on the power of lookaheads. Early on in our MCTS work, we tried a greedy search algorithm that would look one move ahead and pick the children that had scored in the next move. That was enough to get 11 points and fill us with false hope as to how far MCTS might carry us. But it was an early hint that lookaheads are extremely powerful, and that trying to evaluate a well in isolation is less good than considering what the well might be.
This emerged again and again as we progressed through MCTS. Neural networks aided by lookaheads performed better than those without, even when it meant a significant slowdown. It was just never enough to make up for our anemic networks. When it became clear that there was no way to use machine learning to solve HATETRIS and we turned to beam searches, we once again experimented with lookaheads. Unfortunately the sheer overhead of using lookaheads with our beam search meant we were restricted to small beams, and we didn’t really see the utility in lookaheads. It was too impractical when we needed a wide beam. A key mistake, as we now know. Still, it was only with the much faster emulator and a limited lookahead that we got to the full 148 points.
So, if you’re ever exploring a game tree and are wondering if a look ahead is worth it, the answer is probably yes. The other takeaway is that initial intuitions (“hey, lookaheads seem good”) can pan out months or years later, and are thus worth keeping in your back pocket.
The Arrival of Tim
All of this - the development of the new heuristic, the tests on other well shapes, the bird-in-the-hand lookahead - took place over the course of two frenzied weeks, the last week of October 2022 and the first week of November. For there was a deadline. Advent of Code was fast approaching and we knew we’d be out of commission for the duration. (Dave consistently finishes and occasionally places on the leaderboard. Felipe consistently quits around day 10.)
As it turned out, however, our blog post had gotten some notice, and our talk to RustDC had gotten some views. And from the Netherlands, Tim saw the video and took notice. He’d been interested in HATETRIS since our 86 point record in May, but had concluded that to get a fast enough emulator and good enough heuristic to beat us, he’d need to be some sort of Rust expert. It wasn’t until watching our talk that he remembered “Wait a minute - I am some sort of Rust expert!”
Over the first two weeks of November, he coded up his own waveform-based emulator in Rust, with speed comparable to our new cacheless emulator, and devised his own heuristic, with extra terms and extra parameters, and with it got a score of 79 points with a beam width of only 1 million - far better than Knewjade’s heuristic, or ours, for that width. And, as it turned out, he and David had seen each other’s names in the context of Advent of Code; Tim because he consistently places high on the leaderboards each year, and David because he can’t stop writing Advent of Code related poetry. So, Tim contacted us, and we explained the details of the bird-in-the-hand method. After all, science is about sharing results and methodology, and we had nothing to hide.
One day later, Tim posted a new high score: 157 points. We immediately returned to scheming about how we could reclaim the throne. But, as we experimented, we realized that Tim’s heuristic (whose terms he was still improving and modifying) was better than ours, and with more terms came more potential to separate good wells from bad:
| Heuristic Term | Knewjade | Tim |
|---|---|---|
| Holes | ✓ | ✓ |
| Enclosed holes | ✓ | ✓ |
| Enclosed hole lines | ✓ | ✓ |
| Surface height (1x1 piece) | ✓ | ✓ |
| Surface height (S piece) | X | ✓ |
| Heights of leftmost and rightmost columns | X | ✓ |
| Piece erasability | ✓ | ✓ |
| # of squares in the open well unreachable by S-pieces | X | ✓ |
| Deepest row reachable without clearing a line | X | ✓ |
| Deepest row reachable after clearing a line | X | ✓ |
| Score | ✓ | ✓ |
In addition, since none of us were renting any more time on AWS (or any other cloud computing), hardware speed made a difference. His computer had twice as many cores as ours did, and so all else being equal, he could perform a run twice as fast. And with more RAM, he was able to keep a pruned history in memory throughout the whole beam search, making the keyframe generation at the end far faster.
(And the B-trees we were so proud of last time around turned out not to be necessary; Tim realized that while B-trees were great for storing sorted lists, we didn’t actually need to store a sorted list: we only needed a priority queue with the worst element on top, and to compare against that. But, as it turned out, the constant on O(log(n)) was so small that this didn’t affect performance one way or the other.)
Four days later, he posted 170. Sam Hughes’ reaction, on Twitter, was to give a sigh of resignation and declare that this was his life now, posting HATETRIS world record updates every few days, forever. He was not wrong: two days after that, on November 24th, Tim expanded his beam search to 2.5 million and posted an unexpectedly high new score of 232, well above our predictions for the maximum score. We didn’t see it coming at all.
232 was, in fact, another 62-point improvement on the state of the art, just like our 148 point record had been. Tim had now cemented his hold on the record as strongly as we’d cemented ours three weeks earlier. 232 points was a higher score than any of us previously thought possible. It was a record that would last for sixteen hours.
The Return of the King
While we were rediscovering quiescent lookaheads, he studied the blade. While we were busy doing bitwise arithmetic, he mastered sparse matrix multiplication. And while we were improving our Rust emulator speed by a factor of ten, he was improving his neural net speed by a factor of a thousand. Knewjade was back.
Knewjade had seen our 148-point game at the beginning of November, and had sent us his congratulations. He was eager to learn how we did it, and mentioned that he had just a few hours earlier started his latest “non-heuristic approach”…but canceled it, having seen our new score. Victory at last. Our opposition demolished, we could retire in glory.
Except for the small detail that, in the interest of transparency, we explained to him exactly how the bird-in-the-hand heuristic worked. And it turned out that that was the final piece knewjade needed for his new method to exceed all known manual heuristic formulae.
The End of Genesis T.N.K. Evolution Turbo Type D
Back in 2017, the machine learning program AlphaZero was first announced as getting world-class results in Chess, Go, and Shogi, from first principles and without using any existing knowledge of the game. This caused quite the stir; some wondered if it could be used to choose hateful Tetris pieces, while others wanted to - and did - replicate the effort in an open-source way for Go and for Chess.
These open source efforts were born of the fact that while AlphaZero is wildly impressive, it requires corporate level resources to build and train. Most of us don’t have a basement full of Google TPUs and if we did, the power cost to run them would be overwhelming. Like we would re-discover, most of these researchers wanted a way to achieve comparable results without millions of dollars sacrificed on the altar of the cloud. There were two main thrusts in the effort to get around the requirements of AlphaZero: distributed computing, where the training would be done by thousands of volunteers contributing GPU and CPU time, and novel neural architectures that would require less data and thus less resources.
However, Shogi was a different story. The computer Shogi scene was much smaller than either of the other two games AlphaZero was known to be good for, and to train a world-class AlphaZero-type neural network for Go and Chess, it took hundreds or thousands of computers training for quite some time to do it. Shogi simply didn’t have enough people or enough hardware to replicate the effort the same way…but that didn’t stop everybody. In 2018, Japanese Shogi enthusiast Yu Nasu released his first version of a comparably strong neural net, in a program called “The End of Genesis T.N.K. Evolution Turbo Type D”, a program whose name would fit perfectly as the title of a 90s anime. The core of this program was a new neural network, which could be evaluated on a CPU in under a microsecond per move, far faster than AlphaZero’s network and without requiring any kind of GPU or special tensor-mathematics hardware. He called this an Efficiently Updateable Neural Network, or NNUE for short.

NNUE
In a complex network like AlphaZero, hundreds of layers of neurons are stacked on top of each other and evaluated in sequence, one after the other. With hardware like GPUs and TPUs which can evaluate a whole layer at once, this can be made to be relatively fast, but without that type of hardware (or without enough of it), these networks take so long to evaluate that they become the bottleneck. Most of the program’s runtime gets spent waiting for neural networks to finish evaluating. AlphaZero’s core premise is that if the network is good enough, it’s worth the wait; with a good enough neural network, evaluating a thousand positions gets you more insight than evaluating a million positions with something faster but worse.
NNUE is the opposite. Where AlphaZero is classified as “deep learning”, due to the many layers of neurons stacked on top of each other, NNUE is “shallow learning”, with as few layers as possible. Instead of the complexity being stored in dozens of layers of neurons (with each layer being relatively small), the complexity is stored in one enormous layer, right at the start, and the network is only a few layers deep.
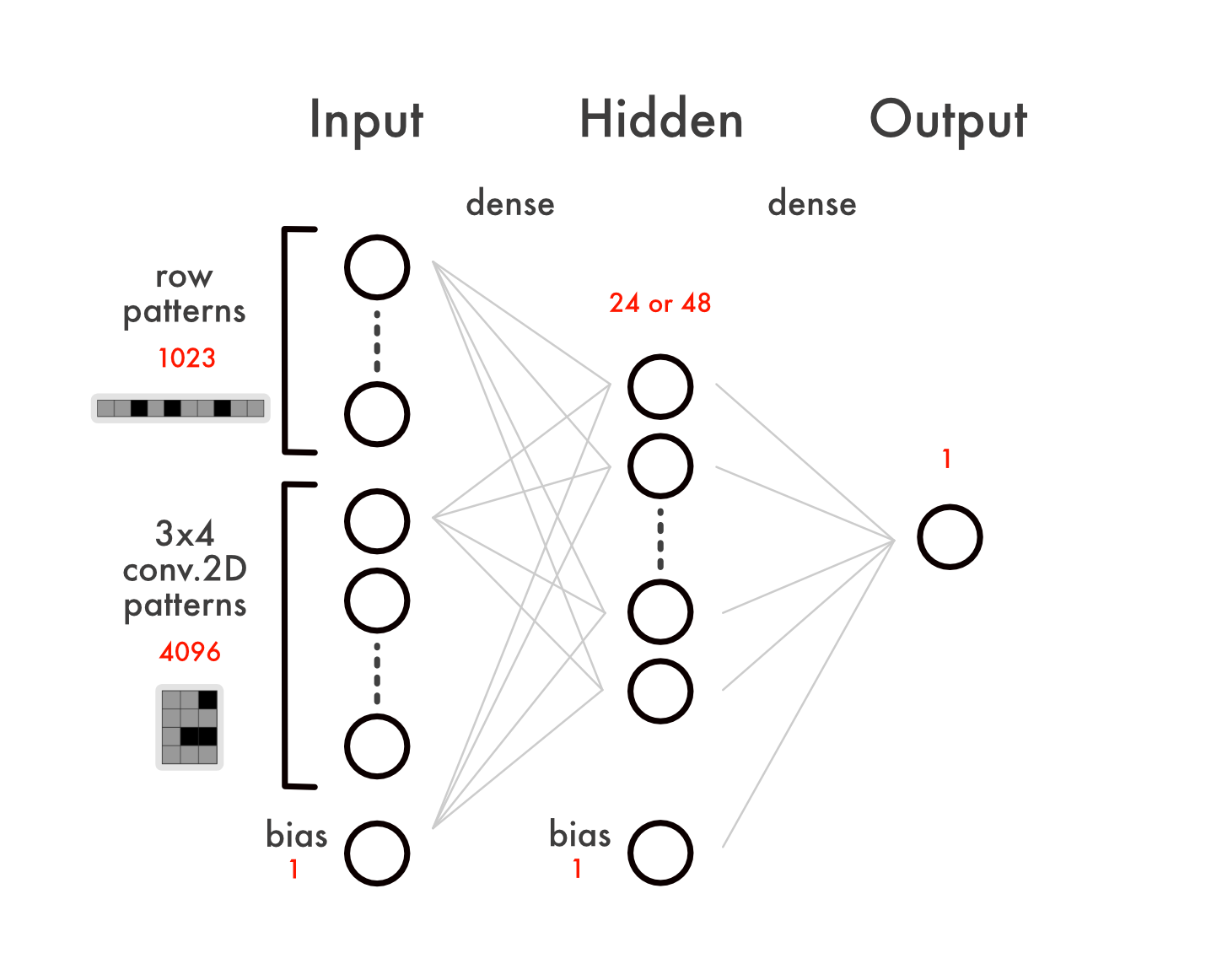 Source: Knewjade
Source: Knewjade
All else being equal, the more weights a neural network has, the more complex it is. A shallow but very broad network (like NNUE) should then be around as complex as a deep but relatively narrow network (like AlphaZero), and in theory, the two should be roughly as powerful when properly trained.
There’s an obvious objection to this: if the network’s just as complex, if it will take just as long to evaluate, then why bother? The answer is sparsity. The fundamental insight behind NNUE is that a very broad network that is sparse can skip most of the calculations every time it’s evaluated. If only 1% of the input neurons are not zero, then only 1% of the weights for that first broad layer have to be calculated…and the network would run 100 times faster than it otherwise would. And that makes it possible to take a project that would normally need hundreds of computers and do it on just one.
This is just a broad strokes overview. The implementation details include even more optimizations, from the accumulator allowing for incremental changes, to carefully tuning assembly instructions to do an operation on 32 or 64 integers with a single command. A lot of work has been done to make NNUE competitive with AlphaZero, and in many ways it has succeeded.
Yu Nasu published his paper in 2018, but as it was in Japanese and specific to a fairly niche game, it didn’t get much attention in the English-speaking world, even after Dominik Klein translated it into English. A year later, Hisayori Noda tried it out for Chess, and was successful enough that Stockfish incorporated it soon after, but for whatever reason, the technique didn’t become common knowledge in the neural network world, and never made the kind of impact AlphaZero did. Certainly, we had never heard of it when we started this project back in 2020. But knewjade had.
AlphaHATETRIS Resurrected
So, by November of 2022, there had been quite a few methods used to get (or attempt to get) the world record:
- Knewjade’s 41, 45, and 66 point records were achieved with beam searches.
- Our 86 point record pre-processed the input into convolutions.
- Tim’s 157, 170, and 232 point records used the bird-in-the-hand lookahead.
- Our attempts at AlphaZero involved backpropagating neural networks based on game tree results.
- Our attempts at speeding up the emulator involved sparse matrix multiplication.
And Knewjade decided that he was going to use all of the above.
Fundamentally, the problem with our AlphaHATETRIS program was that it was too slow. It took us over two weeks to generate a million data points; this was because the neural network (even on a GPU) was fairly slow, and this was because we could only use a small fraction of the data points we actually gathered in a given game. But the core idea was to tell a network “If you did play out a full game, here’s the score you would have gotten”. We wanted to train a network’s ‘intuition’, to get it to only look at good moves.
Knewjade’s approach was different. Instead of trying to train on entire games - far too time consuming - he trained directly on a beam search. And instead of telling the network “here’s the score you would have gotten in a full game”, he told the network “here’s how good a position you would have found if you’d played for another ten moves”. At no point did score come into it at all. Take a wide beam search, and take eight thousand positions from that beam search at random. For each position, play ten moves. At the end of those ten moves, if the game has ended, then that position was pretty bad; give it the worst possible ranking of -1. If the game has not ended, however, then give the position whatever the best ranking of its best descendant was.

It’s difficult to explain just how elegant an approach this is. We’ve seen the power of lookaheads with the bird-in-the-hand heuristic. Knewjade effectively made a network equivalent to playing the previous network with a 10-deep lookahead…and then made another network equivalent to playing that one while looking 10 moves ahead. And then a third, and then a fourth. He didn’t need to worry about score, or try to optimize hyperparameters. The very start of a game was +1. The very end of a game was -1. Everything else was something in between. That’s all his network needed to know.
16 hours after Tim published his record of 232 points from a 2.5-million wide beam, Knewjade published his neural network’s latest result, on a beam a tenth the size: 289 points.
But even 289 points paled in comparison to what he would have gotten were it not for a 2021 rule change to HATETRIS. Without a change in how HATETRIS handles repeated positions, the score would have been ∞. Knewjade had, for the first time, triggered HATETRIS’ loop-prevention rule. The impossible had happened.
Infinite Loop
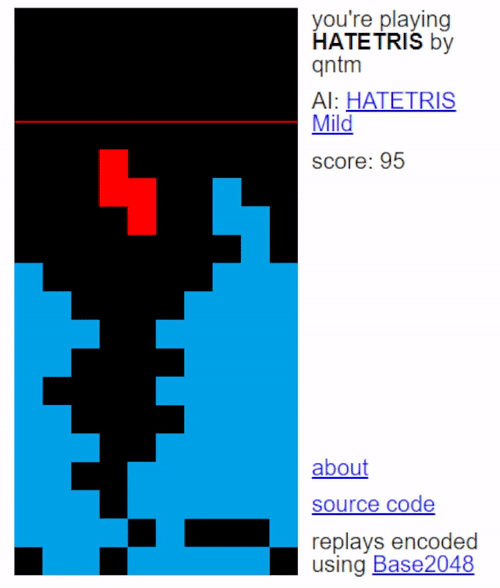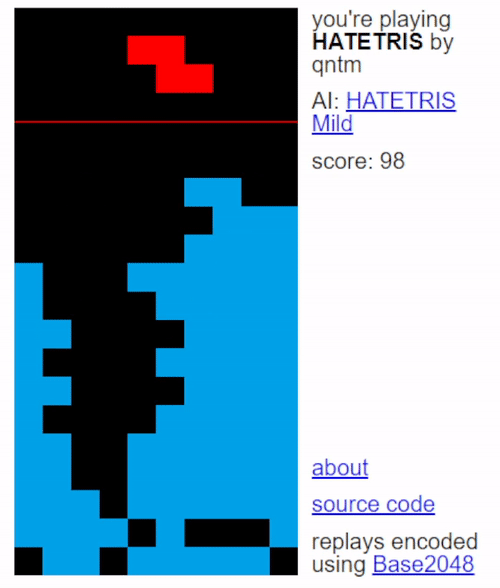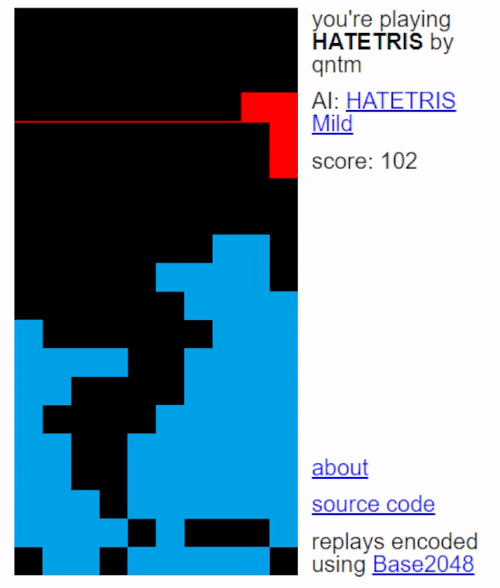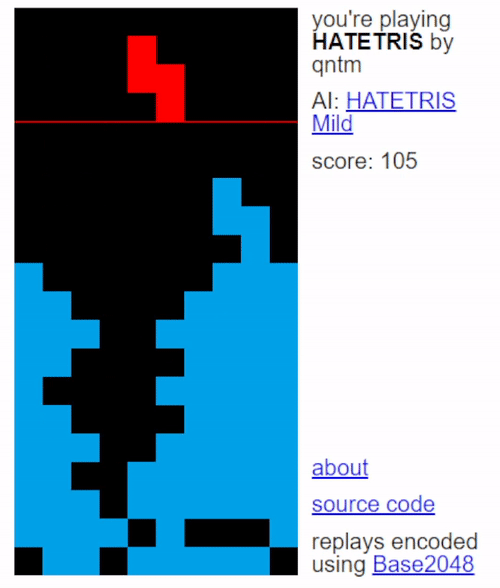
The loop-prevention rule in HATETRIS adds another layer to the way pieces are selected. First, every possible player move for every piece is calculated out. Then, pick pieces with the following priority:
- For each piece, find all wells that can be created with it, and keep track of how many times the most repeated well has been repeated for a given piece.
- Keep only the pieces with the lowest count of well repetition.
- From these pieces pick the piece which causes the highest well for the player.
- If there is a tie, break that tie in the order S, Z, I, O, L, J, T.
For the first year and a half after the introduction of the first rule, it was for all practical purposes as if HATETRIS’ rules had not been changed at all: nobody had ever triggered the loop prevention rule, or even shown it to be possible for a standard-sized 16x10 well. And because we all assumed that the rule could never be triggered, we never bothered putting it into our emulators.
And there was a reason for that, beyond mere laziness. The second, third, and fourth rules of HATETRIS rely only on the arrangement of blocks within the well - everything you need to know can be derived by a glance at the well shape. But the first rule, the loop-prevention rule, relies on the entire history of the well. In a beam search, it is far more efficient not to store the history of a given well - until it’s time to get the keyframes at the end of the game - and even if you store the history, it takes a long time to go through that entire history and check against every single well you’ve ever seen to see if there are duplicates.
So having to do this for every possible legal move of every current position would be very, very, slow. The 5 μs per move emulator we were so proud of two sections ago just wouldn’t matter anymore; the vast majority of the runtime would be spent checking the well histories, only for well over 99.99% of them to not be repeats anyway. And this means that all naive emulators, like ours, would become utterly useless the instant they run into an infinite loop - the behavior predicted by the emulator would no longer be the same as the behavior exhibited in the actual game.
This is what happened to Tim, the next day. Still fresh from his 232 point game and working on further improvements to his heuristic, he stumbled on an infinite loop of his own, causing Sam Hughes to make a second leaderboard for loops, ranked by amount of cleared lines required to enter a repeat state. Upon seeing that (and with the start of Advent of Code looming), Tim decided to bow out of the high score contest, content with a score two hundred points above the world record a mere two years prior. Modifying his emulator to efficiently check for repeat states was a bridge too far for him.
Knewjade, in his writeup, ended with a challenge to all future HATETRIS attackers:
That’s it, this article ends here. Just one last word.
If there are people who improve on this method as a foundation, there is no problem at all, and I am happy about that. However, personally, if possible, I would like to add some kind of ingenuity to it.
Looking at the score, we agreed - now that a would-be infinite loop had been discovered, and now that the score was almost 300 points, no future game was ever going to be impressive purely because of a high score. And so, between that and the start of Advent of Code, we decided to join Tim, and leave the leaderboard where it was.
Dangling Threads
And that would seem to be the end. Knewjade declared that his method could be used to get scores as high as anyone could want, and Sam Hughes, for his part, declared on Twitter:
HATETRIS is entirely broken open at this point, I think. It was a hard game, but now it isn’t.
The question we are left with is, I think, the same question that I started with, way back in 2010: how difficult can Tetris get? From this latest work, it may be that the true answer is “not very”
It may be that this aspect of Tetris is essentially over, in the same way that chess AI is essentially over
Each new high score used to be shocking, but now it isn’t; Knewjade, Tim, Sam Hughes, and we all think that much higher scores are possible, and nobody now would be terribly surprised at a 400-point game announced out of the blue. Neural networks can always be made more complex, their training sets can always be made bigger, and up to the true limits of HATETRIS itself, the scores can keep getting asymptotically higher. So, knowing that, what remains to be done? Is the only thing left to do to train networks for years to get more and more lines?
No. There are still more questions to answer than that.
Unanswered Questions
- Are there a huge number of loops possible in HATETRIS, or just a few?
- What well dimensions would allow loops, without the loop prevention rule?
- Is it possible to trigger the loop prevention rule for the same target well more than once?
- Is a true loop (repeating a well state already seen) possible?
- If it is, is it possible to set up in such a way as to allow a four-line clear, since the algorithm in the event of what would otherwise be a true loop HAS to give an I piece if the I piece would lead to a previously unseen well?
- What moves are entropic and cannot be undone, and what moves aren’t?
- Can the bottom line, under any circumstances, be cleared?
- What’s the best strategy that’s actually derivable (or at least comprehensible) by human beings, like Deasuke’s 30-point pseudoloop strategy? Are there pseudoloops that do significantly better?
And all of these questions come down to the same question. HATETRIS, according to many, has been beaten. But can it be understood? And, more broadly, can understanding it be useful outside the esoteric realm of a handful of nerds who are overly invested in it?
Beyond HATETRIS: NNUEvil

And HATETRIS is, itself, just one tiny subset of Tetris, one set of rules for selecting pieces to give to the player. It’s not the only ruleset, or the best, or the hardest possible. Since it is always possible (for a well of width 10) to force the game to end, we know that the hardest possible piece selection for Tetris would not need a loop prevention rule. If you hit a loop, ever, then you didn’t give the correct piece the first time around. So, another set of questions becomes natural: what is the hardest version of Tetris possible? And how hard would it be?
Imagine a hypothetical game of Tetris - call it NNUEvil. In it, a neural network much like the one knewjade used to get 289 points would select pieces to provide to the player. Right now, HATETRIS calculates the lowest possible well heights for each piece, and gives the player the piece with the highest of those. NNUEvil would do something very similar, but would take the best heuristics for each piece, and give the player the piece with the worst best-case scenario. And in the same way that our HATETRIS algorithms all check to see if a well can be cleared with repeated S-pieces, NNUEvil would check all combinations of pieces that could clear consecutive lines, to make it much harder to set up more than one line clear in a row. We strongly suspect this would, if made, be much harder than HATETRIS. It would probably work. But there would be downsides.
NNUEvil would be slow. Slower than HATETRIS already is. It takes time to evaluate moves, especially if you have to do a move rollout. This is not a problem when you consider a single human playing the game, but it is a problem if someone wants to say… run a massive beam search using some custom heuristic. Time, we’ve learned, is the greatest enemy in trying to explore a complex game tree, and adding even a half a second computation per move would slow things down significantly.
A further challenge is that NNUEvil would just not be fun for human players. HATETRIS is already not fun for human players, as evidenced by the fact that there isn’t much interest in people playing it, as opposed to computational solutions. There isn’t a side community competing for the best human derived answer. Thus it would be an exercise in creating an adversarial network for other networks to fight against. We’re all about robot cage matches, but its questionable if the effort of building and deploying NNUEvil would result in any interesting emergent behavior.
Because, fundamentally, what makes HATETRIS interesting, is a series of coincidences and engineering decisions that have it toe the line between “actually impossible” and “trivially easy”. It was not known for the first twelve years of HATETRIS whether or not an infinite loop was possible (or, when the loop prevention rule was added, whether or not that rule could ever be triggered). We know that for small enough well sizes, loops are impossible, and for all we know as of 2023, a height of 16 might be the very smallest height in which a loop can be made. If Tetris had slightly different pieces, it’d be impossible to force even a single line; if the pieces of HATETRIS were in a slightly different order, it’d be trivially easy to force infinite lines. HATETRIS is a very simple set of rules that leads to very complex behavior. That’s interesting, in a way that NNUEvil wouldn’t be.
Finally, there’s the question of training. A perfectly evil algorithm would be always learning, always improving, but there is a maximum somewhere, a point where our network has reached its local maximum and the only way to improve it is risking it getting worse. Without a way to prove that NNUEvil has achieved maximum evil, there would always be the need to continue to explore the training space. This moving goalpost would mean records would be quickly invalidated, and the question of “is this even its final form?” would always be at the back of the minds of those trying to beat its current iteration.
It would be a step in the right direction, but it’s not clear how much we or anybody else could really learn from it. The true goal would be not a quantitative improvement in algorithmic hatefulness, but something more qualitative, and something more final.
HATETRIS: The Endgame
- Is there a way to calculate, for a given line, what the minimum piece sequence is to clear it?
- So far, no one has ever cleared the bottom line of a well in HATETRIS, though every other line can be cleared. Is the bottom line possible to clear? And if not, can this be proven?
- Does Bruztowski’s algorithm admit a mathematical solution with the tools we have available, and an optimum strategy and highest possible score?
- If so, what is that high score?
- Can we derive the maximum score for HATETRIS the same way?
- Can we derive the maximum score for Tetris - in general, with perfectly adversarial piece selection - in that same fashion?
Answering those questions would be where things would truly get interesting. If you think that it sounds challenging to figure out the math behind these things, you would be right! We have some vague intuitions and ideas based on having looked at a lot of wells, and if someone were to get serious about this, the starting point would probably be to gather as much well data as possible for systematic analysis. That said, we are not mathematicians. A formal proof is outside of the scope of our competencies.
So what are our guesses? We believe that you can assign every well and every move on a well an entropy value that represents its progress towards a finite end state. After all, even the best networks eventually lose, so if no permanent infinite loop is possible every move must, to some degree, increase entropy. How do you calculate that? You could make it a fraction, the number of moves remaining over the number of moves in the longest possible game… if you had a fully explored tree and knew how many moves could remain for all possible children. Since that fully explored tree is functionally impossible to have (without a breakthrough in supercomputing or infinite time), you have a problem. A heuristic can only be an approximation and that’s not going to cut it here.
It’s possible that there is only a small number of well states that potentially lead to loops. Understanding those shapes and how they relate to repeated s-clears would likely give us some kind of better understanding of well structure and its relationship to entropy and line clears.
One possibility, based on the bird-in-the-hand heuristic, is that the proof would involve the surfaces of wells. Some wells have a surface reaching all the way down to the bottom. Some wells have surfaces higher than that which can be lowered to the bottom (or at the very least, lowered beyond their current height) after one line clear, or two line clears, or three, or more. But some wells have surfaces that can’t be moved down, and finding surfaces that can’t be moved down is a harbringer of the end of the game.
But, “can’t be moved down” is a bit of a misleading phrase. If the height of the well were drastically increased in the middle of a game, there are many surfaces which “couldn’t be moved down” before that suddenly could be. It’s not that it’s impossible to move down those surfaces, it’s that the well isn’t high enough to do it. There is some minimum number of moves needed to clear these surfaces, and an infinitely high well would let us see that minimum number. And finding a way to measure that, to measure the minimum number of moves needed to bring any given surface down by a line, and the minimum height the pieces need to stack up to in order to perform those moves, would probably be the first step. We don’t have a name for this. Line-entropy? Meta-entropy? Line-height-removal-required? Regardless, there is some value which captures “the amount of height needed so that a line is potentially clearable”, and to be clear, some lines may be unclearable, that value could be infinite. We don’t know, and have very little idea of how to find out barring extreme experimentation.
This would be hard. But so far, everything we’ve done in HATETRIS has taught us something valuable, be that Rust itself, or machine learning, or bitwise optimization, or GPU integration, or the math behind neural network backpropagation, or the importance of memory contiguity for CPU cache speed. And this line of attack, if pursued and if possible, would probably teach as much about math as the hunt for the HATETRIS world record has taught about programming. We’re probably not the people to do it, but you, reader, might.
The Power of Collaboration
Not everything we learned about programming from HATETRIS was something we came up with ourselves. In fact, at this point, nobody who has had the HATETRIS world record in recent history has done so completely alone. Knewjade started off by improving on chromeyhex’s 31 point record, coming up with a better endgame when he didn’t yet have the tools to make a whole game from scratch. We started off by improving Knewjade’s heuristic, before finding the quiescent bird-in-the-hand lookahead that let us shoot much further. Our old blog post gave Tim what he needed to come up with a better heuristic still, and it gave Knewjade the idea that pre-processing wells into convolutions was a viable strategy for neural network training.
And anyone just starting now would have all of that, both a working expert heuristic and a working neural network training routine, and could build on it in a way that perhaps none of us would have thought of ourselves.
HATETRIS itself is not important. Not really. It doesn’t matter in any material sense what the high score is, or who has it. But for people like us, who have worked on HATETRIS for maybe a day or maybe a year, it does matter how we spend our time. How we act is important even if what we do isn’t.
It is a strange thing when we consider it, that of most of the great enterprises which men undertake, what they would consider the mere accidents are often the most important results, and the enterprises themselves, their success or failure, are in truth but accidents. How many men realize that by far the most important result of the business they are engaged in, which taxes all their powers, mental and physical, is not whether it succeeds or fails, but whether it makes them honest or dishonest, thorough or slipshod, generous or mean…
Basil W. Maturin, Self-Knowledge and Self-Discipline
There’s a small, mean-spirited part of every person that thinks things like sportsmanship, honor, and fighting fair don’t matter, not in the face of winning. It would have been trivial for us to hide everything we did. To produce tweets with increasing numbers and incredible games and never speak a word as to the how.
And if we had, the world record would still be in our hands. We might even still have discovered the bird in hand heuristic. But the game would be poorer for it, and so would we. By being free with our knowledge, we made things harder for ourselves, undoubtedly, but we also learned more and had a more enjoyable time than we ever would have otherwise.
But if knewjade had never written about getting the world record in HATETRIS, the record would remain at 66, and neither Tim nor we would have ever had the chance to explore the fascinating world of HATETRIS, and the four of us would never have built on each other’s work to push the record this far. Knewjade could have kept it all to himself, and held onto the record indefinitely. He didn’t, and the field is better off for it.
Except, that’s not the whole story either.
 Source: Threepipes
Source: Threepipes
In 2019, a coder named threepipes, inspired by a QuizKnock video featuring HATETRIS, decided as a small coding class project to try to get the world record in HATETRIS. Making an independent emulator is an awful lot of work, so instead he extracted the Javascript code from the actual game and built a python framework around the Javascript API calls. He came up with the basic idea of a heuristic beam search and used it, but due to hardware limitations (and the unavoidable slowness of Javascript), he was only able to achieve a handful of games between 15 and 18 points, a far cry from the 31 point record of the time.
This looks at first glance like a failure. He didn’t get the world record, he didn’t come up with any new strategies for playing the game, and he didn’t even beat what the best human players had come up with by hand almost a decade earlier. But, crucially, he wrote about what he did and he published it online. Two years later, knewjade stumbled across that slideshow, and the basic idea of a heuristic beam search gave knewjade some inspiration of his own. The current state-of-the-art record-breaking HATETRIS techniques ultimately derive from a class project written by someone who played around with the game once and then never touched it again.
The pursuit of knowledge can feel futile. There are endless struggles, and sometimes we fall short of the mark. However, when we make the effort to write it down, to leave a beacon that others can follow, it can turn what feels like a failure into a success, by guiding the way for others.
Appendix: The New Emulator
This is a section that didn’t fit anywhere else. Its technical, a bit dry, and just not very in tune with the narrative…but it’s also very useful if you’re trying to implement your own emulator, so here it is.
Cached Waveforms
In HATETRIS, rotating a piece four times gets the piece back to where it started. Moving a piece left and then moving it right again, likewise moves it back to its original position. The only irreversible move is ‘down’. So, it makes sense to group positions by how many times the piece has moved down. We call those groups of positions ‘waveforms’, and represent them with binary - every position in a group has a corresponding bit in the waveform, and that bit is a 1 if the position is possible, or a 0 if the position is not possible.
 If you read part 1, this gif will be familiar.
If you read part 1, this gif will be familiar.
For each piece except the O piece, in a standard 20x10 well, there are 34 possible positions per waveform (the O piece has 36), and the insight we had for our previous emulator was that if you had a given waveform, and a given 4x10 slice of a well, and you moved every piece in that waveform down, the new waveform you’d generate would always be identical. Some positions would be blocked and be unable to move down, some positions would not be blocked, and which positions were blocked and which weren’t would always be the same if the waveform and the 4-line slice of the well were the same. So, if we could store waveforms and slices of wells in a cache, we could look up what the next waveform would be and what the legal positions would be, rather than go through the time-consuming process of calculating them again.
Click or hover for more details
This was fast, but the process of doing even a single HashMap lookup to find the waveform from the cache became one limiting factor - HashMap calls are slow, on the order of a couple microseconds each, even if you use tricks like a custom hasher to speed them up. The flamegraph is clear on that. For quite a few months, we’d discussed the possibility of doing waveform calculations without a cache somehow - if we could, that would be quite the improvement. But to do waveform calculations without a cache, we’d need to go into bitwise arithmetic.
Cacheless Waveforms
We represent a waveform as a 34-bit integer (padded out to 64 bits, since nobody makes 34-bit processors), and each 1 and 0 represents whether a specific position is possible or impossible. If there was some mathematical operation or sequence of operations, that would take a waveform at height h in the well and generate the waveform at height h+1, that would in theory remove any need for a cache - the cache lookup would just be a slower version of what these math operations would be doing.
We started with small pieces: we did not attempt to brute-force a magic number we could multiply the waveform by to generate the next one. If we took a waveform at height h, moved it down to height h+1, pruned out all the positions that were now not legal, and then did as many left, right, and rotate operations on the positions in that waveform as we could, then we’d have the waveform we wanted at height h+1. So, there were four operations we needed to figure out:
- Move every position in a waveform left
- Move every position in a waveform right
- Rotate every position in a waveform
- Remove all positions in a waveform that intersect blocks already in the well.
The problem was that a waveform is just a single 64-bit binary integer - we weren’t storing lists of positions whose internal values we could modify, and we only had one bit to work with per position. If our waveform was (abcdefghi), and moving every position left created the new waveform (00ehibdc0), we’d have to somehow find binary operations we could apply to (abcdefghi) to create (00ehibdc0), regardless of what values digits a through i actually were. From (000000000) to (111111111), the operation would have to always transform the waveform the same way and get the correct output.
And this was daunting - daunting enough that we went with the cache instead. Figuring out what operations would generate these arbitrary permutations would be a real challenge, and we didn’t have enough experience with bitwise arithmetic to be confident doing it. The cache was nearly a tenfold speedup, after all, so why go with something even harder?
Eureka Moment
But, that’s where having the chance to sit back and reflect helped. Finding operations to generate arbitrary permutations, for us novices, was difficult. But what if the permutations weren’t arbitrary? What if we made sure the waveform had patterns we could use?
For our redefined waveform, each waveform consisted of n-1 blocks of 4 moves, sorted by x-offset and rotation, where n is the width of the well. For instance, a well of width 6 will have a waveform of 5 blocks and 20 total bits, like so:
w = abcd efgh ijkl mnop qrst
In other words, we gathered by x-offset and then by rotation. Some of these positions will never be possible, even in an empty well. Some of these will stick out of the well to one side or the other. That’s perfectly fine. We’re doing 64-bit operations anyway; so long as the waveform remains smaller than 64 bits, each operation will take the same amount of time regardless.
So, with waveforms that actually had structure, suddenly the left and right operations became easy. Taking a waveform and moving it left, moving it right, or rotating it, now visually had a pattern:
1
2
3
4
w_old = abcd efgh ijkl mnop qrst
w_left = efgh ijkl mnop qrst 0000
w_right = 0000 abcd efgh ijkl mnop
w_rotate = bcda fghe jkli nopm rstq
The left operation corresponded to multiplying w_old by 16 - or, equivalently, shifting all of its bits four to the left - and then cutting off the four most significant bits. The right operation corresponded to dividing w_old by 16 - or, equivalently, shifting all of its bits four to the right.
And the rotate operation, which was the one we were really worried about, can be split in two:
1
2
3
w_old = abcd efgh ijkl mnop qrst
w_rotate = bcd0 fgh0 jkl0 nop0 rst0
+ 000a 000e 000i 000m 000q
So, that was the first three operations we needed. The only operation we still needed to figure out was making sure every bit in the waveform that corresponded to an illegal position was 0.
Bitmasking
We already store wells as arrays of binary integers. So, a line of a well is a single 16-bit integer. A four-line slice of a well is four 16-bit integers. For a well of width 6, it would look something like this:
1
2
3
4
[a1 b1 c1 d1 e1 f1]
[a2 b2 c2 d2 e2 f2]
[a3 b3 c3 d3 e3 f3]
[a4 b4 c4 d4 e4 f4]
For a well of width n, there are (2^n)-1 possible lines. For width 6, there are 63 possible lines; for width 10 (the actual HATETRIS width), there are 1023. This is not bad at all - modern computers have no difficulty in storing 1023 64-bit integers in memory. So, what this means is that for all 1023 possible lines, we generate a mask: a new 64-bit integer, where each bit corresponds to a waveform position. If that waveform position intersects that line (or else goes outside of the well), the bit is 0. If that waveform position does not intersect that line, the bit is 1. When generating a new waveform, we look up the four masks corresponding to the four lines in our four-line slice of a well, and use bitwise AND to combine them all. Only if a position does not intersect any of the four lines is it legal.
For instance, take this slice of a well of width 6:
1
2
3
4
0 0 0 0 0 1
0 1 0 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
The mask m for this slice would be:
1
new_mask = masks[000001][1] & masks[010001][2] & masks[110001][3] & masks[100001][4]
And now we have all four pieces, and with the new mask new_mask and the old waveform w_old, we can generate the new waveform w_new:
1
2
3
4
5
6
7
8
9
10
11
12
w_new = w_old & new_mask
w_tmp = w_new
while w_tmp > 0:
w_right = w_new >> 4
w_left = w_new << 4
w_rotate: (w_new & 011101110111...) << 1 |
(w_new & 100010001000...) >> 3
w_new |= w_right
w_new |= w_left
w_new |= w_rotate
w_new &= new_mask
w_tmp = w_new & !w_tmp
Piece Legality & Score Checking
So, we now have all waveforms, for any piece we like, for any well we like. To find out a list of all reachable positions for a given piece, just run that waveform calculator, and keep moving the new waveforms down one row at a time until the waveform is 0, meaning that no reachable position is that low. And to find out which of those reachable positions correspond to ‘moves’, compare each waveform with the waveform below it: a position which is reachable but which cannot go down is a ‘move’.
So, the next problem is: how do you determine which of the seven pieces the HATETRIS algorithm will actually give you? Well, in the absence of loop prevention (fortunately, loops are impossible, so we don’t need to worry about loop prevention), the HATETRIS algorithm will give you whichever piece of the seven generates the highest well, assuming you place the piece as low in the well as you can. The worst best-case scenario, in other words.
There are two components to the final height of a move: the shape of the piece (and where the move is placed in the well), and how many lines that move clears, if any. If a move does clear a line, everything above that line gets moved down, which lowers the height of the well. But, as the flamegraph showed, just generating all those wells from all those moves and allocating enough memory to store them all was the primary bottleneck for the emulator speed. Somehow, we’d have to figure out how many lines each piece in a waveform scored, and how high each piece was within the well, without allocating more memory or actually creating new wells. Ideally, we don’t want to create any new wells until we know which piece the emulator’s actually going to give us.
To make a long story short, that’s what we did. In a similar way to bitmasking to find intersections between pieces and wells, we created more bitmasks to determine move heights and line clears, and used those bitmasks to determine the legal moves without actually making the wells corresponding to those moves. It was much more involved and tedious than the first stage was, but it followed the same principles, and in the end we didn’t even need the hundred-and-ten-line match statement that we manually wrote out for every possible case.
You can find the full implementation on Github here; the neural network implementation is questionable, but as mentioned in the TL;DR, the emulator worked. Really well, and really fast. For the month in which it remained viable.

Comments powered by giscus.